物理学基础 6:静电场中的导体与电解质
基础
静电平衡的导体内部场强为零:
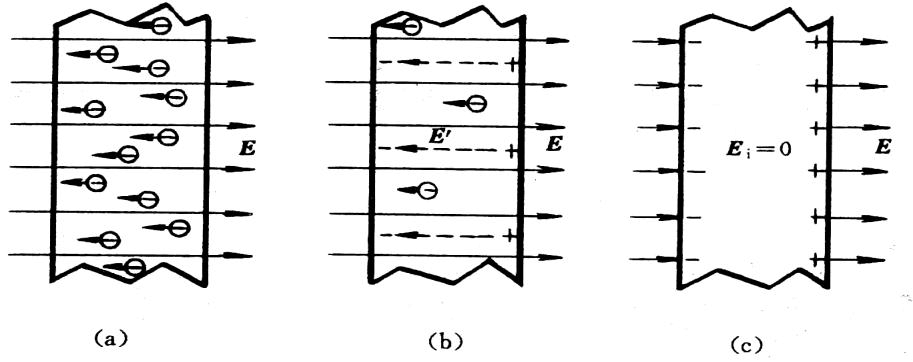
原因:内部电子自由移动形成了反向电场,抵消了外部的电场。
例题
【例子】 有一空气平行板电容器,电容为C,两极板间距为d,充满电后两极板间的相互作用力为F,则两极板间的电压为_,正极板带电量为_。
【分析与解答】
F = \frac{QE}{2} = Q \frac{U}{2d}\\
Q = CU
$$
所以 $ U = \frac{2dF}{Q} = \frac{Q}{C} $,所以 $ Q = \sqrt[]{2dFC}, U = \frac{Q}{C} = \sqrt[]{\frac{2dF}{C}}$
【例子】 一空气平行板电容的两极板面积均为S,两板的间距为d,在两板间平行地插入一面积也是S、厚度为t的金属片(t < d),请问电容C是多少?
【分析与解答】
$ C = \dfrac{\varepsilon _0 S}{\Sigma \frac{d_i}{\varepsilon _{r_i}}} $
两个极端:空气的 $ \varepsilon _r = 1 $,金属板的 $ \varepsilon _r = + \infty $
对于本题:
C = \frac{\varepsilon _0 S}{\frac{d - t}{1} + \frac{t}{+\infty }} = \dfrac{\varepsilon _0S}{d - t}
$$
【例子】 推导圆柱形电容器的电容公式。已知介质 $ \varepsilon _r$ ,内外半径 $ R_1, R_2 $,高度是 L。
【分析与解答】
选取一段子圆柱面作为高斯面。
假设线密度是 $ \lambda $,那么 $ Q = \lambda \Delta L $
根据高斯定理 $ \Phi = \dfrac{Q}{\varepsilon _0} =\dfrac{\lambda \Delta L}{\varepsilon _0} = E 2 \pi r \Delta L $
于是得到
E = \frac{\lambda }{2 \pi r \varepsilon _0}
$$
而
C = \dfrac{Q}{U} = \frac{Q}{\int_{R_1}^{R_2} \dfrac{\lambda }{2 \pi \varepsilon _0 } \frac{1}{r} \mathrm{d}r} = \dfrac{Q}{\dfrac{\lambda }{2 \pi \varepsilon _0} \ln \frac{R_2}{R_1}}
$$
所以得到 $ C = \dfrac{2 \pi \varepsilon _0 L }{\ln \dfrac{R_2}{R_1}} $,考虑到介质不是真空,置换后得到:
C = \dfrac{2 \pi \varepsilon _0 \varepsilon _r L}{\ln \frac{R_2}{R_1}}
$$
【例子】 已知球形电容器 $ R_1 < R_2 $,介质为真空。求其电容。
【分析与解答】
根据高斯定理
\Phi = E \cdot S_n = E \cdot 4 \pi r^2 = \dfrac{Q}{\varepsilon _0}\\
\Rightarrow E = \frac{Q}{4 \pi \varepsilon _0 r^2}
$$
而 $ Q = C \cdot U = C \cdot \int_{R_1}^{R_2} E \mathrm{d}r = C \cdot \dfrac{Q}{4 \pi r^2}(\dfrac{1}{R_1} - \dfrac{1}{R_2})$
两边约去 $ Q $,得到 $ C = 4 \pi r^2 \varepsilon _0 \dfrac{R_1R_2}{R2 - R_1} $
【例子】 一带负电荷的金属球,外面同心地罩一不带电的金属球壳,则在球壳中一点 P 处的场强大小与电势(设无穷远处为电势零点)分别为
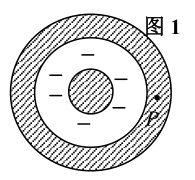
【分析与解答】 静电平衡的导体内部场强为零。场强的话是积分到无穷远处,单看球壳内对场强的贡献是 0,但是到了外边会产生一个球形放射电场,电场线指向球心。电势为负。
