谈谈牛顿迭代法
从开根说起
如何用牛顿迭代计算 $\sqrt[]{2}$ ?
首先,此问题相当于求 $x_0, \text{ s.t. } x^2 = 2 \quad x > 0$
即,求函数 $f(x) = x^2 - 2$ 的零点。
牛顿的思想是,任取一个点 $(x_1, y_1)$。经过这一点的切线是:
$$ y - y_1 = f^\prime (x_1) ( x - x_1 ) $$于是此切线的零点 $x_2 = - \dfrac{y_1}{f'(x_1)} + x_1$
可以看到,下图的 $(x_2,0)$ 已经很接近 $f(x)$ 的零点。
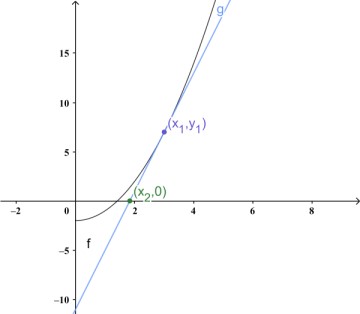
于是,我们重复这一过程。取 $(x_2, y_2)$ ,求其切线与 $x$ 轴的交点 $x_3$ ……
上面的过程只要反复迭代,就能将 $|x_n - x_0|$ 不断缩小。
$f ^ \prime (x) = 2x$ ,因此对于本问题的牛顿迭代公式为:
$$ x_n = x_{n-1} - \dfrac{y_{n-1}}{2x_{n-1}} $$取初始值 $x_1 = 2$ :
-
$(x_1, y_1) = (2,2)$ , $x_2 = 2 - \dfrac{2}{4} = \dfrac{3}{2}$
-
$ ( x_2, y_2 ) = (\dfrac{3}{2}, \dfrac{1}{4}), x_3 = \dfrac{3}{2} - \dfrac{1}{4} \cdot \dfrac{1}{3} = \dfrac{17}{12}$
-
$(x_3, y_3) = (1.41666666667, 0.00694444444), y_x = 1.41421568628$
对比一下:
-
$x_0 = 1.41421356237$
-
$y_4 = 1.41421568628$
经过短短三次迭代,就已经精确到了小数点后 5 位,可见效率之高。
代码实现:
1double sqrt(double n) {
2 const double delta = 1E-10;
3 double x = 1;
4 while (true) {
5 double xn = (x + n / x) / 2;
6 if (abs(x - xn) < delta) {
7 break;
8 }
9 x = xn;
10 }
11 return x;
12}
这里有必要提一下_平方根倒数速算法_
1float Q_rsqrt( float number )
2{
3 long i;
4 float x2, y;
5 const float threehalfs = 1.5F;
6
7 x2 = number * 0.5F;
8 y = number;
9 i = * ( long * ) &y; // evil floating point bit level hacking
10 i = 0x5f3759df - ( i >> 1 ); // what the fuck?
11 y = * ( float * ) &i;
12 y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
13// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
14
15#ifndef Q3_VM
16#ifdef __linux__
17 assert( !isnan(y) ); // bk010122 - FPE?
18#endif
19#endif
20 return y;
21}
感兴趣的话,可以读这篇文章。
