详解编辑距离（Levenshtein 距离）算法

目标

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

说实话，我看不懂 LC 上的题解——虽然看完能照猫画虎代码，但是对于原理还是不清不楚。不给实例分析的题解都是耍流氓（暴论）。

概念铺垫

代表串：假设有字符串 w，则下标 i 处的字符为 w[i]，其代表串为 w[i]之前的子串（切片） w[0:i-1]（也即 w 从头算起长度为 i 的子串）。

举个例子，现有字符串 pluveto，则 w[3] 代表串为 plu。w[0] 代表串为 $\varepsilon$ （空串）。

【定义】 $f(i,j)$ 表示将 w[i] 代表串，变成 w[j] 代表串所需的最小步骤数。

这里的步骤，就是执行操作的个数，允许的操作已经在题目中给出。

DP 表的解释

以下面的表为例，从上到下是 i 增加的方向，从左到右是 j 增加的方向。坐标从 0 起（对应轴上的空白），比如下面写着 0 的格子，其坐标是 $(0,0)$.

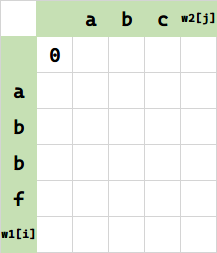
初始化 DP 数组，尝试寻找规律

$f(0,0)$ ，将 (空串) 变成 (空串) 需要 0 步，无脑填 0.

$f(0,1)$，将空串变 a 需要一步插入，填 1.

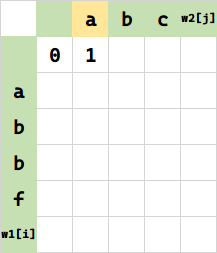
f(0,2)，将空串变 ab 需要两步插入，填 2. 相当于 $f(0,1) + 1$。

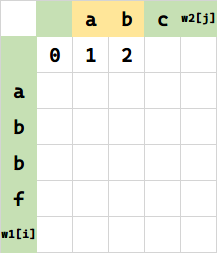
同理：

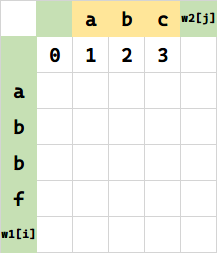
接下来，将 f(1) 所代表的串 a 变成空串，需要 1 步删除。

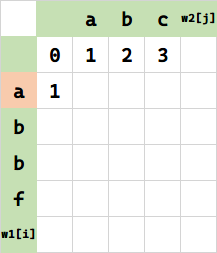
同理，将 (2,0) 代表的串 ab 变成空串，需要 2 步删除。相当于 $f(1,0)+1$。

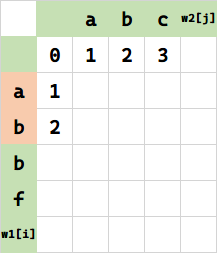
其余同理。

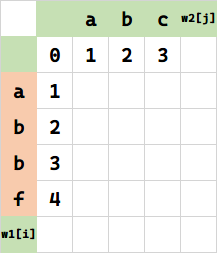
归纳：如何利用历史状态计算新状态？

重点来了。下面我们填写 $f(1,1)$。即将 w1[1] 的代表串 a 变成 w2[1] 的代表串 a（本次求值目标）。

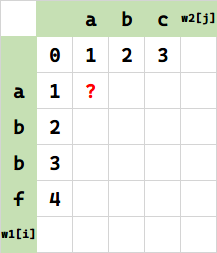
（请时刻关注上面这个求职目标的位置）

我们有三种操作的方法，插入，删除，替换，对应三种情况：

插入的情况

第一种情况，先将 w1[i-1] 代表串变成即 w2[i] 代表串。需要 f(0,1)=1 次操作：

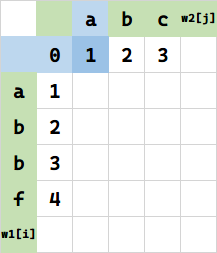
这种操作之后，再将 w1[i-1] 代表串之后插入一个 a，即可得到本次求值目标。这种情况下 $f(1,1) = f(0,1) + 1 = 1+1=2$。

其中 f(1,1) 表示本次求值目标，

f(0,1) 表示 w1[i-1] 代表串变成 w2[i] 代表串所需次数，查表得到 $1$。

1 表示 w1[i-1] 代表串之后再插入一个 a 这一次动作的计数。

替换的情况

第二种情况，先将 w1[i-1] 代表串（空串）变成 w2[i-1] 代表串（空串）。需要 f(0,0)=0 次操作。

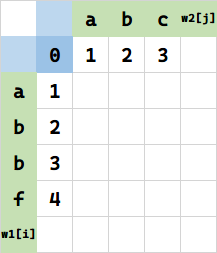
然后再把 w2[i] 代表串替换为 w1[i] 即可得到本次求值目标，实现两串相同。由于替换的字符恰好等于 w2[i] 的字符，即不需要替换，即代价为 0。这种情况下，$f(1,1)=f(0,0)+0=0$.

删除的情况（等价于插入）

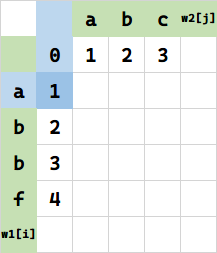
第三种情况，先将 w1[i] 代表串 a 经过变成 w2[j-1] 代表串（空串）。查表需要 f(1,0)=1 次操作。

然后再在w2[j-1] 代表串（空串）之后插入一个 a 即可得到本次求值目标，这种情况下，进行了一次操作，代价为 1，$f(1,1)=f(1,0)+0=1+0=1$.

也可以理解为在 w1[i] 最后删除一个 a，对 w2 插入和对 w1 删除就代价和效果而言是等价的

上面三种操作，代价最小的是第二种，所以我们取 $f(1,1)=\min(1,0,1) = 0$：

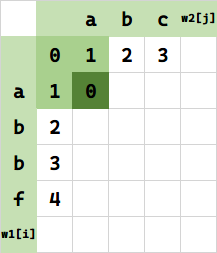
发现，实际上求 $f(i,j)$，就是求左上角、正上方、正左方的（单元格的值各自与其对应后续操作的开销的和）的最小值： $\min\{f(i-1,j) + c_1,f(i-1,j-1)+c_2,f(i,j-1)+c_3\} = \min(C_1,C_2,C_3)$

有个细节在于 $c_1,c_2,c_3$ 的计算。$c_1,c_3$ 是插入和删除操作（或者可以都看成插入），开销固定是 1.

$c_2$ 是替换操作，w1[i] == w2[i] 即字符相同时不用替换，开销是 0，不同时替换，开销是 1.

至于为啥？

为了读者更好地理解，我们不糊弄过去，下面看个例子。求值目标是 $f(i,j) = f(3,2)$：

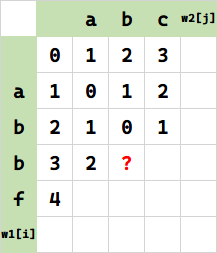
在这一步发现。周围开销最小的是上方，即 $f(i-1,j)=f(2,2)=0$，即意味着，只要经过 0 步，就可以把 w1[i-1] 代表串 ab，变成 $w2[j]$ 代表串 ab. 这没问题。此时 w1[i]==w2[j]=='b'，我们怎么办？

我们令 $C_1 = f(i-1,j) + c_1$ $C_2 = f(i-1,j-1) + c_2$ $C_3 = f(i,j-1) + c_3$

怎么求 $C_1$ ？让 w1[i-1] 代表串 ab 变成 w2[j] 代表串 ab 的开销是 0，要经过一步插入，所以 $c_1 =1$，$C_1 = 1+1=2$
同理让 w1[i] 代表串 abb 变成 w2[j-1] 代表串 a 的开销是 2（上表 $f(i,j-1)$），然后要经过一步删除，所以 $c_3 =1 $，$C_3 = 2+1=3$
再看 $C_2$，由于 $f(i-1,j-1)$ 即让 w1[i-1] 代表串（ab）变成 w2[j-1] 代表串（a）的开销是 $f(i-1,j-1) = 1$，而 w1[i]==w2[j]，所以 $c_2 = 0$，故 $C_2 = 1+0 = 1$

所以 $f(i,j) = \min \{C_1,C_2,C_3\} = \min\{2,1,3\} = 1$：

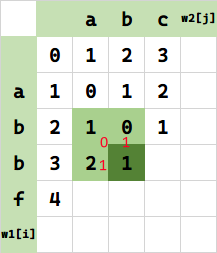
重复此过程，得到：

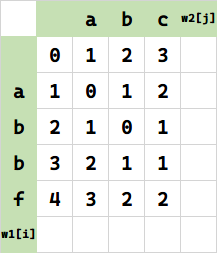
最右下角就是答案：

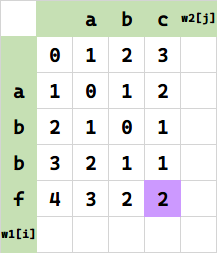
用代码表达出来

掌握了手算的方法，剩下的就是代码实现。

参考代码：

 1inline int min3(int a, int b, int c) {
 2  return a < b ? (c < a ? c : a) : (b > c ? c : b);
 3}
 4
 5class Solution {
 6public:
 7  int minDistance(string w1, string w2) {
 8    int n = w1.size();
 9    int m = w2.size();
10    vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
11    // -- 初始化基本情况
12    // +-------> y
13    // |
14    // x
15    //
16    // 第一列的各行
17    for (int i = 1; i <= n; i++) {
18      dp[i][0] = i;
19    }
20    // 第一行的各列
21    for (int j = 1; j <= m; j++) {
22      dp[0][j] = j;
23    }
24    // -- 开始 DP
25    for (int i = 1; i <= n; i++) {   // 各行
26      for (int j = 1; j <= m; j++) { // 各列
27        auto c1 = dp[i - 1][j] + 1;  // 上
28        auto cc2 = w1[i - 1] == w2[j - 1] ? 0 : 1;
29        auto c2 = dp[i - 1][j - 1] + cc2; // 左上
30        auto c3 = dp[i][j - 1] + 1;   // 左
31        dp[i][j] = min3(c1, c2, c3);
32      }
33    }
34
35    return dp[n][m];
36  }
37};

空间优化

$f(i,j)$ 只依赖当前行和前一行。但是初始化的时候却要初始化最左列全部。如果优化为 $O(m)$ 空间，势必要破坏最左列的初始化。但是注意到初始化的结构和遍历的结构很像，只要把“第一列的各行”初始化放到后面就行：

 1class Solution {
 2public:
 3  int minDistance(string w1, string w2) {
 4    int n = w1.size();
 5    int m = w2.size();
 6    int d = 2;
 7    vector<vector<int>> dp(d, vector<int>(m + 1, 0));
 8    // 第一行的各列
 9    for (int j = 1; j <= m; j++) {
10      dp[0][j] = j;
11    }
12    // -- 开始 DP
13    for (int i = 1; i <= n; i++) { // 各行
14      dp[i % d][0] = i; // 初始化移动到这儿了
15      for (int j = 1; j <= m; j++) {      // 各列
16        auto c1 = dp[(i - 1) % d][j] + 1; // 上
17        auto cc2 = w1[i - 1] == w2[j - 1] ? 0 : 1;
18        auto c2 = dp[(i - 1) % 2][j - 1] + cc2; // 左上
19        auto c3 = dp[i % d][j - 1] + 1;
20        dp[i % d][j] = min3(c1, c2, c3);
21        // print_vec_2d(dp);
22      }
23    }
24
25    // print_vec_2d(dp);
26
27    return dp[n % 2][m];
28  }
29};

优化后的空间复杂度变成 $O(2m)$，有所进步。

进一步空间优化

我们还可以进一步优化为 $O(m)$，即只用一个额外数组。画个图就懂了：

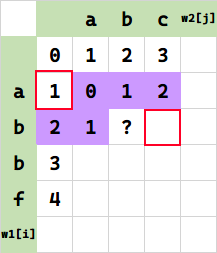
可以注意到，每一步所依赖的范围，只有这一行的元素个数+1，即 $m+1$。其余左上角前面的值、问号后面的值是什么，我们并不关心。据此，可以滚动这个 m+1 的空间求值。

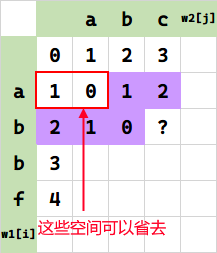
下面是进一步优化的结果：

 1class Solution {
 2public:
 3  int minDistance(string w1, string w2) {
 4    int n = w1.size();
 5    int m = w2.size();
 6    if (n == 0)
 7      return m;
 8    if (m == 0)
 9      return n;
10    std::vector<int> dp(m + 1);
11    for (int c = 0; c < m + 1; c++) {
12      dp[c] = c;
13    }
14    for (int r = 1; r < n + 1; r++) {
15      int pre = r;
16      for (int c = 1; c < m + 1; c++) {
17        int cur = min(dp[c], pre) + 1;
18        if (w1[r - 1] == w2[c - 1]) {
19          cur = min(cur, dp[c - 1]);
20        } else {
21          cur = min(cur, dp[c - 1] + 1);
22        }
23        dp[c - 1] = pre;
24        pre = cur;
25        if (c == m)
26          dp[c] = cur;
27      }
28    }
29    return dp[m];
30  }
31};