物理学基础:1-2 圆周运动
PS: 斯坦福把这一部分作为第六章,我们则当做第一章第二小节,不得不佩服苏联模式下的学生都是大(gan)佬(di)。
法向加速度
法向加速度是怎么来的?公式又如何推出?
在圆周运动中,我们一直被教以:切向加速度改变速度速度大小,法向加速度改变速度方向。但是后者对我来说很难理解,我花了很长时间才弄明白。下面我们来探究一下。
首先,什么是加速度?加速度是 $\vec{v}$ 对 $t$ 的导数:
\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} \tag{1}
$$
而速度可以表示为 速度大小乘以切向矢量:(切线是 tangent,故有角标 t)
\vec{v}=v\vec{e_t}\tag{2}
$$
带入 (1) 中,可得:
\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} \tag{1}=\frac{\mathrm{d}(v\vec{e_t})}{\mathrm{d}t}
$$
(注意要用链式法则)也即:
\vec{a} = \frac{\mathrm{d}v}{\mathrm{d}t}\vec{e_t} + v\frac{\mathrm{d}\vec{e_t}}{\mathrm{d}t}
$$
加号左边 $\dfrac{\mathrm{d}v}{\mathrm{d}t}\vec{e_t}$ 是切向加速度。(带入 $v=\omega r$ 还可得到角加速度)
加号右边 $v\dfrac{\mathrm{d}\vec{e_t}}{\mathrm{d}t}$ 中,$\dfrac{\mathrm{d}\vec{e_t}}{\mathrm{d}t}$ 表示切向单位向量的变化率。什么?单位向量还有变化率?实际上考虑旋转变换,单位向量随时间转圈圈,一个无穷小时间 $\mathrm{d} t$ 内,转过了 $\mathrm{d}\theta$ 度,对比前后的两个向量,确实是产生了一个差向量。把它记作 $\Delta\vec{e_t}$
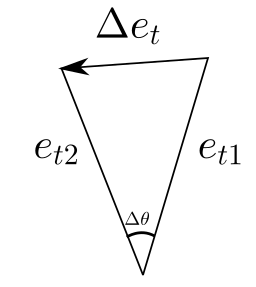
(注:下面所说的圆都是极限情况的曲率圆,也就是曲线密切圆)
可以看到,当 $\Delta \theta \to 0$ 时,$\Delta e_t \perp e_{t1}$ $\Delta e_t$指向圆心。什么,指向圆心?我们需要换个角度看问题:
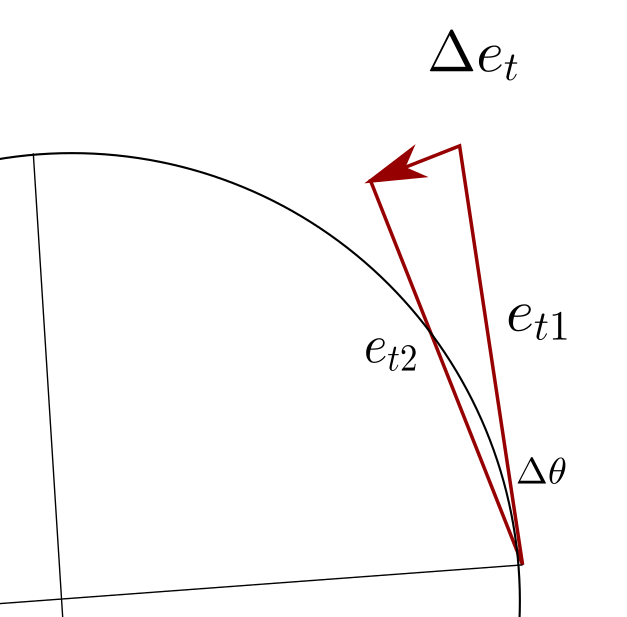
箭头那里就是单位向量的变化量。可以发现 $\Delta \theta \to 0$ 的时候它确实指向圆心。
根据弧长公式:$\Delta e_t = \Delta \theta \cdot r$。$r = |e_{t1}| = 1$ (单位向量),由于指向圆心,还要乘以一个方向单位向量来赋予它方向的含义,也即:$\Delta \vec{e}_{t} = \Delta \theta e_t \cdot \vec{e_n}$ ,其中 $\vec{e_n}$ 是指向圆心的单位向量——法向向量。
而
\lim _{\Delta t \rightarrow 0} \frac{\Delta \vec{e}_{t}}{\Delta t}=\frac{\mathrm{d} \vec{e}_{t}}{\mathrm{d} t}
$$
带入可得:
v\frac{\mathrm{d} \vec{e}_{t}}{\mathrm{d} t}=v\frac{\mathrm{d} \theta}{\mathrm{d} t} \overrightarrow{e_{n}}
$$
等式右边,正是法向加速度表达式。
回过来看那个链式法则推出来的加速度表达式:
\vec{a} = \frac{\mathrm{d}v}{\mathrm{d}t}\vec{e_t} + v\frac{\mathrm{d}\vec{e_t}}{\mathrm{d}t}
$$
可以发现,正是 切向加速度+法向加速度。
现在我们得到的表达式则是:
\vec{a} = \frac{\mathrm{d}v}{\mathrm{d}t}\vec{e_t} + v{\color{blue}\frac{d \theta}{d t} }\overrightarrow{e_{n}}
$$
你会发现 ${\color{blue}\dfrac{d \theta}{d t} } = \omega$ ,带进去之后可以得到:
圆周运动加速度公式
\bold{a} = \bold{a_t} + \bold{a_n}
$$
其中:
\left\{\begin{aligned}a_{t} &=\frac{\mathrm{d} v}{\mathrm{d} t} e_{t}=\alpha _r e _t \\a_{n} &=\frac{v^{2}}{r} e_{n}=\omega^{2} r e_{n}\end{aligned}\right.
$$
