«自动机理论、语言和计算导论»笔记:终章 重点小结
题型
区分文法
乔姆斯基把方法分成四种类型,即0型、1型、2型和3型。
0:无任何限制。
1:再限制每个 $\alpha \to \beta$,都有 $|\alpha|\geq|\beta|$(上下文有关)
2:再限制每个$\alpha \to \beta$,$\alpha$ 都是非终结符。(上下文无关)
3:再限制 $A \to \alpha | \alpha B$ (右线性),或者 $A \to \alpha | B \alpha$(左线性)。(线性文法)
4:
构造文法识别简单语言
简单有序数量关系型
【例】构造右线性文法识别 $L = \{a^{3n+1} | n \geq 0\}$
区分左线性文法和右线性文法
右线性文法,非终结符在右边,例如
$S\to aB$,迭代之后字符串从右边展开。
分析:
我们可以写出符合规定的字符串。
$$
\begin{align}
w_1 &= a\\
w_2 &= aaaa\\
w_3 &= aaaaaaa
\end{align}
$$
可以观察到:
$$
\begin{align}
w_1 &= a\\
w_2 &= aaa w_1\\
w_3 &= aaa w_2
\end{align}
$$
易知 $w_i = aaaw_{i-1}$ 对于 $i>1$ 总是成立。故递推规则如下:
$$
\begin{align}
S &\to a\\
S &\to aaaS
\end{align}
$$
解答:
$$
G = (N, T, P, S), \text{ where } N = \{S\}, T = \{a\}, P:
$$
$$
\begin{align}
S &\to a\\
S &\to aaaS
\end{align}
$$
无序数量关系型(a 的个数是 b 的 N 倍)
【例子】 构造 CFG 识别 $L = \{w| w \in \{a, b\} 并且 a 的数量是 b 的 2 倍\}$
分析:
这种我们一般用插空法。首先写出最简单的情况:
$$
\begin{align}
S &\to \varepsilon \\
S &\to aab| aba | baa
\end{align}
$$
然后往三个基本形式的空位里插入 S 即可。(至于是不是有重复,肯定是有的,但是咱也不管了)
$$
S \to SaSaSbS| SaSbSaS | SbSaSaS
$$
解答:
$$
G = (N, T, P, S), \text{ where } N = \{S\}, T = \{\}, P:
$$
$$
\begin{align}
S &\to \varepsilon \\
S &\to aab| aba | baa \\
S &\to SaSaSbS| SaSbSaS | SbSaSaS
\end{align}
$$
任意串型
变形:以 p 开头 q 结尾型。中间就是任意串型,套一下就行了。
【例子】 识别 $L = \{w|w \in \{0,1\}\}$
分析: $S \to 0S|1S$
设计 DFA
前后缀型
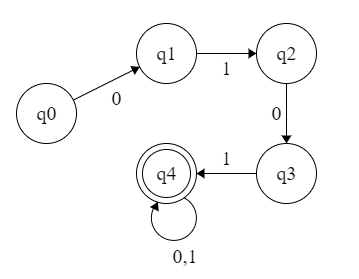
【例子】 识别 {0,1} 上以 0101 开头的串。
分析:需要用一个状态做开始,N(缀长)个状态做记忆。
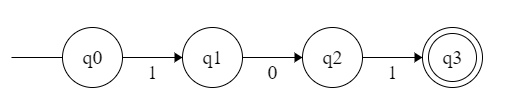
【例子】 识别 {0,1} 上以 101 结尾的串。
我们很容易想到这样结尾的:
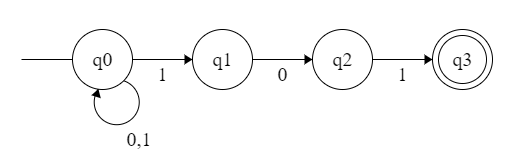
但是有个问题,万一我输入 1010,照样被接受了。这种情况下如果用 NFA 就会很好设计:
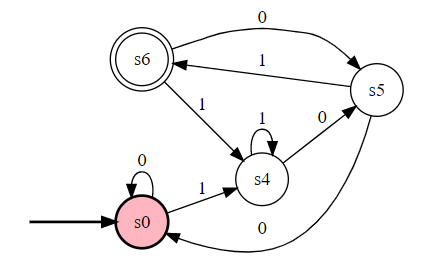
这种题,我们先设计出 NFA,然后转换为 DFA 即可。结果为:
包含序列型
【例子】 识别 {0,1} 上包含 101 的串。
很容易设计出 NFA:
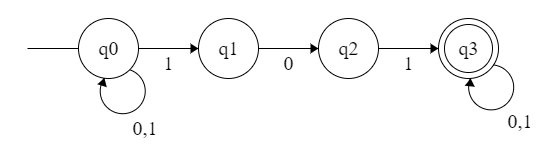
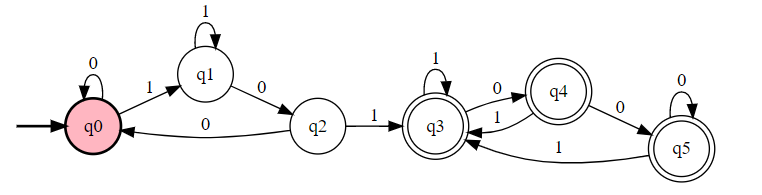
所以转换为 DFA 就行了。
幂集构造化简结果:
All States: q0({q0}),q1({q0,q1}),q2({q0,q2}),q3({q0,q1,q3}),q4({q0,q2,q3}),q5({q0,q3})
Input Symbols: 0,1
Transition Function:
delta({q0}, '0') = {q0}
delta({q0}, '1') = {q1}
delta({q1}, '0') = {q2}
delta({q1}, '1') = {q1}
delta({q2}, '0') = {q0}
delta({q2}, '1') = {q3}
delta({q3}, '0') = {q4}
delta({q3}, '1') = {q3}
delta({q4}, '0') = {q5}
delta({q4}, '1') = {q3}
delta({q5}, '0') = {q5}
delta({q5}, '1') = {q3}
Initial State: q0
Final State: q3({q0,q1,q3}),q4({q0,q2,q3}),q5({q0,q3})
当然,这里也有一些取巧的方法,例如重置状态法。使用于类似检测连续相同序列的情况。
【例子】字母表 $T = \{a,b\}$,找出识别含有 3 个连续 b 的所有字符串的集合的 DFA。
分析:我们用三个状态存储 1 个 b,2 个 b,3 个 b 的情况。一旦出现输入 a 就重定向到 0 状态,除非已经达到 3 状态。状态机如下:
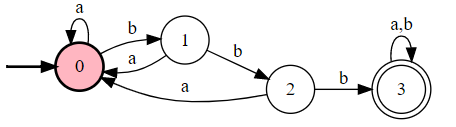
不包含序列型
【例子】 识别 {0,1} 上不包含 101 的串。
构造规则语言
$L$的补$L'$的 DFA,只需要将原语言的接受、非接受状态对调即可。
根据补语言的构造方法以及上题结果,答案如下:
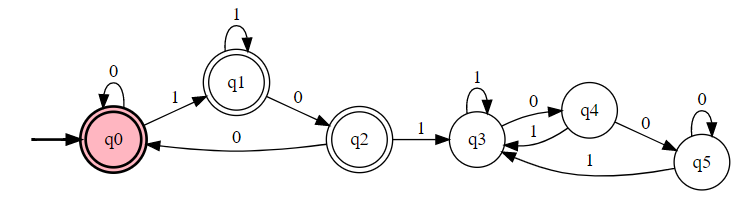
多次包含序列型
$T = \{a,b\}, L = \{w \mid w 至少含两个 b,至多一个 a\}$
这种题不太好直接设计,建议先写出正则式,然后转 DFA。
分析:可能的情况:
-
b*bbb* -
ab*bbb* -
b*abbb* -
b*babb* -
b*bbab* -
b*bbb*a
利用后面的方法转换为 DFA。
DFA 的转换
NFA 转 DFA(幂集构造)
见:自动机的幂集构造法详解 | 更少的幺蛾子 (less-bug.com)
生成式(规则文法)转 RE
牢记 R 规则:
R = aR + b <=> a*b
$G_{1}=(\{S, A, B, C\},\{a, b, c, d\}, P, S)$, 其中生成式如下:
$$
\begin{align}
S &\rightarrow b a A \quad S \rightarrow B\\
A &\rightarrow a S\\
A &\rightarrow b B\\
B &\rightarrow b\\
B &\rightarrow b C\\
C &\rightarrow c B\\
C &\rightarrow d\\
\end{align}
$$
解答:
C = cB + d
B = b + bC = b + b(cB + d) = bcB + bd + b = (bc)*(bd + b)
A = aS + bB = aS + b(bc)*(bd + b)
S = B + baA = (bc)*(bd + b) + ba(aS + b(bc)*(bd + b))
= baaS + (bc)*(bd + b) + bab(bc)*(bd + b)
= (baa)*((bc)*(bd + b) + bab(bc)*(bd + b))
衍生题型**: RE 构造右线性文法**,正则集构造右线性文法。
例子:以 abb 结尾的字符串的集合。字母表是 $\{a,b\}$ .
分析:
容易写出正则式 S = (a+b)*abb
S = (a+b)*abb = (a+b)S + abb + e
等价关系:
$(a^*b^*)^* \Leftrightarrow (a^*+b^*)^* \Leftrightarrow (a+b)^*$思考:怎样证明?(提示:用集合包含关系)
RE 转 DFA
一般方法:先从 RE 生成 $\varepsilon $-NFA,然后转换为 NFA,再转换为 DFA。
然而这种过程非常繁琐,通常我们可以取巧用状态添加法。
【例子】c*a(a+c)*b(a+b+c)*+c*b(b+c)*a(a+b+c)* 可以识别 $\{a,b,c\}$ 上包含至少一个 $a$ 和至少一个 $b$ 的串的集合。画出它的状态机。
分析:
先画出起始状态和中止状态:
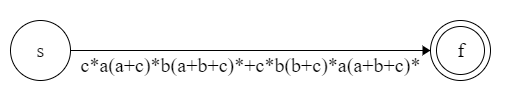
对正则进行合并:
c*a(a+c)*b(a+b+c)*+c*b(b+c)*a(a+b+c)*
=c*[a(a+c)*b | b(b+c)*a](a+b+c)*
观察可知,c* 一个边,a(a+c)*b 和 b(b+c)*a 各一个边,最后 (a+b+c)* 一个边:
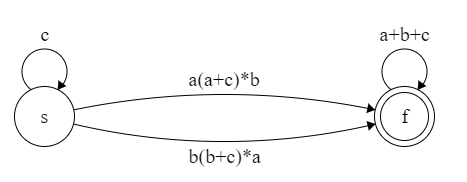
对两条边继续添加状态:
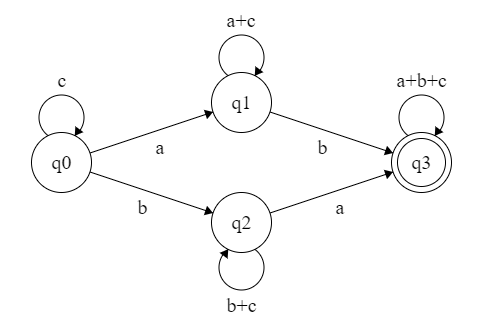
标准化:
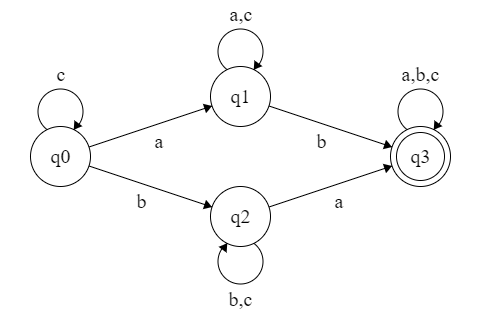
DFA 转 RE
通常使用状态消除法。关键在于分析节点的来源去路,遍历组合,用等效的规则式替换。
DFA 的化简
可使用填表法。例如 ch13 习题 16.
泵浦引理的证明题
// todo 例如 ch13 习题 17.
米兰机和摩尔机
米兰机在转移时输出
摩尔机在到达时输出
构造米兰机
【例子】输入为 $\{0,1,2\}$ 上的串。输入一个三进制数时,输出此输入模 4 的余数。
| 三进制数 | 模4余数 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 10 | 0 |
| 11 | 1 |
| 12 | 2 |
| 13 | 3 |
| 20 | 0 |
可以观察到,模 4 余数就是最后一个输入的数。首先想到的思路是无条件跳转。但是问题在于,这样对于状态 0 需要跳转到
构造摩尔机
摩尔机转换为米兰机
米兰机转换为摩尔机
CFG 的化简
消无用符号
能产生
$\varepsilon$的符号也是有用的!
【例子】$G$:
-
$S\to A \mid B$ -
$A\to aB \mid bS \mid b$ -
$B\to AB \mid B a$ -
$C \to AS \mid b$
分析:
首先 找有用非终结符。
唯一的终结符是 $b$.
$A,C$ 能一步推出 $b$,是有用的。
$S$ 能推出 $A$ ,是有用的。
最终 $B$ 是无用的。
结果:
-
$S\to A$ -
$A \to bS \mid b$ -
$C \to AS \mid b$
【例子】将 $G_1, G_2$ 变换为没有无用符号,且与其等价的上下文无关文法。
$G_1$:
-
$S\to DC \mid ED$ -
$C\to CE\mid DC$ -
$D\to a$ -
$E\to aC\mid b$
解:
| 迭代次数 | 有用符号 |
|---|---|
| 0 | $a,b$ |
| 1 | $a,b,D,E$ |
| 2 | $a,b,D,E,S$ |
因此 $C$ 是无用符号。结果$:
-
$S\to ED$ -
$D\to a$ -
$E\to b$
消空生成式
【例子】$G$ 的 $P$:$S\to aSbS \mid bSaS \mid \varepsilon$,求其无 $\varepsilon$ 文法 $G_1$.
解:
显然 $S$ 是可致空符号。针对 $aSbS$,$bSaS$,代入 $S$ 空或非空的情况。(简记为 00,01,10,11)
| 原始串 | 00 | 01 | 10 | 11 |
|---|---|---|---|---|
| aSbS | ab | abS | aSb | aSbS |
| bSaS | ba | baS | bSa | bSaS |
因此有:$G_1 = (N_1, T, P_1, S_1)$
新的产生式为:
P_1:
S -> ab
abS
aSb
aSbS
ba
baS
bSa
bSaS
S_1 -> $
S
$N_1 = N \cup \{S_1\}$
消单生成式
消左递归
直接代公式:
$A\to A \alpha_1 | \beta_1$ 变换为
-
$A\to \beta_1 | \beta_1 A'$ -
$A'\to \alpha \mid \alpha C'$
CFG 的转换
CFG 转 Chomsky 范式(CNF)
【例子】将下列文法转为 CNF。
$$
\begin{align}
S &\to bA|aB\\
A &\to bAA|aS|a\\
B &\to aBB|bS|b
\end{align}
$$
分析:
令 $B_b \to b, B_a \to a, B_1 \to BB, B_2 \to AA$ ,有:
$$
\begin{align}
S &\to B_bA|B_aB\\
A &\to B_bB_1|B_aS|a\\
B &\to B_aB_2|B_bS|b
\end{align}
$$
所以 CNF 为:
$$
\begin{align}
S &\to B_bA|B_aB\\
A &\to B_bB_1|B_aS|a\\
B &\to B_aB_2|B_bS|b\\
B_b &\to b\\
B_a &\to a\\
B_1 &\to BB\\
B_2 &\to AA
\end{align}
$$
【例子】$P$: $S\to aAB \mid BA$, $A \to BBB \mid a$, $B\to AS\mid b$,已经是无$\varepsilon$,无循环,无无用符号,无单生成式的文法。求等效 CNF $G_1$.
分析:
使 $C_a \to a$,则 $S\to C_a AB$。
再使 $C_1 = AB$,则 $S\to C_a C_1$
使 $C_2 = BB$,则 $A\to C_2B$
此致。
【例子】求文法 $G$ 的等效 CNF,其中 $P:$
-
$S\to A\mid B$ -
$A\to aB\mid bS \mid b$ -
$B \to AB\mid Ba$ -
$C\to AS \mid b$
分析:
第一步,消无用符号。
- b,A,C 有用。B 无用,得:
-
$S\to A$ -
$A\to bS | b$ -
$C \to AS \mid b$
发现 $C$ 不可达。得:
-
$S\to A$ -
$A\to bS \mid b$
第二步,消单生成式。$S\to bS \mid b$
最后求 CNF,增加 $C_b \to b$,则 $S\to C_b S \mid b$
CFG 转 Greibach 范式(GNF)
GNF 的构成步骤
CFG 转 CNF
将终结符排序。对
$A_i \to A_j \beta\quad (j < i)$的进行代换,直到$A_i \to A_1 \beta$消左递归
回代
【例子】将下列文法转为 GNF。
$$
\begin{align}
A &\to BC\\
B &\to CA|b\\
C &\to AB|a
\end{align}
$$
显然这已经是一个 CNF。
排序:建立偏序关系 $A < B < C$。对于 $A\to BC$,$B \to CA \mid b$,都满足。但对于 $C\to AB \mid a$,不满足 $C \leq A$,因此将 $A$ 解开得到 $C\to BCB \mid a$。$C\leq B$ 为假,继续变换得到 $C \to CACB | bCB | a$,$C \leq B$ 为真。
阶段结果:
-
$A\to BC$ -
$B \to CA\mid b$ -
$C \to CACB \mid bCB \mid a$
对于 $C \to CACB \mid bCB \mid a$,需要消除左递归。
$C\to a\mid bCB\mid a C' \mid bCB C'$
$C'\to ACB\mid ACB C'$
阶段结果:
-
$A\to BC$ -
$B \to CA\mid b$ -
$C\to a\mid bCB\mid a C' \mid bCB C'$ -
$C'\to ACB\mid ACB C'$
下面进行回代:
C 代入 B:
B -> CA | b
-> aA | bCBA | aC'A | bCBC'A | b
B 代入 A:
A -> BC
-> aAC | bCBAC | aC'AC | bCBC'AC | bC
A 代入 C':
C' -> ACB | ACBC'
-> aACCB | bCBACCB | aC'ACCB | bCBC'ACCB | bCCB |
aACCBC' | bCBACCBC' | aC'ACCBC' | bCBC'ACCBC' | bCCBC'
这样就得到了 GNF:
-
$A\to aAC | bCBAC | aC'AC | bCBC'AC | bC$ -
$B\to aA | bCBA | aC'A | bCBC'A | b$ -
$C\to a\mid bCB\mid a C' \mid bCB C'$ -
$C'\to aACCB | bCBACCB | aC'ACCB | bCBC'ACCB | bCCB |\\ aACCBC' | bCBACCBC' | aC'ACCBC' | bCBC'ACCBC' | bCCBC'$
设计 PDA 识别语言
压栈的表示:
$a,b/cb$表示读入$a$,若栈顶是$b$,则将$c$入栈。出栈的表示:
$a,b/\varepsilon$表示读入 a,若栈顶是 b,则弹出 b。
$z_0$表示栈底标志。
【例子】构造一个 PDA M 接受 $L(M) = \{a^nb^n \mid n\geqslant 0\}$.
分析:
第一种设计,用空栈表示接受。
初态是 q0,每输入一个 a,压栈
b a a
------------------------>
|a |
|z_0 |
+---+
一旦输入一个 b,状态变为 q1,弹出一个 a。
如果此时栈中只剩栈底,则完成
1var stack = []
2/*
3 0: 接受 a
4 1: 接受 b
5 2: 终态
6*/
7var status = 0;
8
9function onInput(char input){
10 // 对 a 压栈
11 if(status == 0 && input == 'a'){
12 status = 1;
13 stack.push(c);
14 // 每输入一个 b,弹出一个 a
15 }else if(status == 1 && input == 'b'){
16 status = 1;
17 stack.pop();
18 }else{
19 reject();
20 }
21 if(isAccepted()){
22 status = 2;
23 }
24}
25
26function isAccepted(){
27 return status == 1 && stack.empty();
28}
转写为数学形式:
$\delta (q_0, a, z_0) = \{(q_1, az_0)\}$
第二种设计,使用终态表示接受。
初态为 q0,当输入 a,将 a 入栈,转到 q1。
q1 下,当输入 b,转到 q2,并弹出 a。
q2 下,当输入 b,转到 q2,并弹出 a,如果弹出的是 z0,则转到 q0,结束。
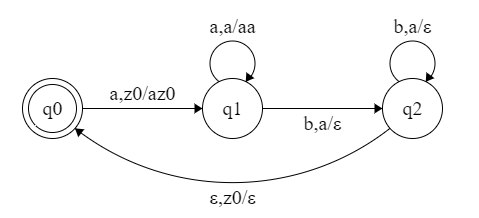
aabb 的识别过程:
| 当前状态 | 输入带 | 栈 |
|---|---|---|
| q0 | aabb | z0 |
| q1 | abb | az0 |
| q1 | bb | aaz0 |
| q2 | b | az0 |
| q2 | $\varepsilon$ |
z0 |
| q0 | $\varepsilon$ |
$\varepsilon$ |
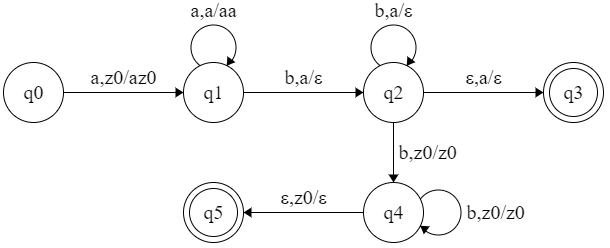
【例子】构造 PDA M,接受 $L(M) = \{a^mb^n \mid m \neq n , m\geq 1,n\geq 1\}$
分析:
使用终态接受
CFG 的相关转换
CFG 转 PDA
【例子】CFG 的产生式:
-
$E\to EOE \mid (E) \mid v \mid d$ -
$O\to + \mid *$
构造接受它的 PDA。
分析:
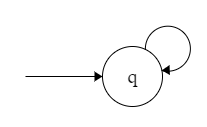
$$
\begin{align}
\varepsilon,E&/EOE\\
\varepsilon,E&/(E)\\
\varepsilon,E&/v\\
\varepsilon,E&/d\\
\varepsilon,O&/+\\
\varepsilon,O&/*\\
a,a&/\varepsilon
\end{align}
$$
$a\in \{(,),v,d,+,*\}$(非终结符)
答:
$M = (\{q\}, \{v,d,+,*,(,)\}, \{E,O,v,d,+,*,(,)\}, \delta, q, E, \phi)$,其中 $\delta$ 定义为:
$\delta(q,\varepsilon,E) = \{(q,EOE),(q,(E)),(q,v),(q,d)\}$
$\delta(q,\varepsilon,O) = \{(q,+),(q,*)\}$
$\delta(q,v,v) = \delta(q,d,d) = \delta(q,+,+)=\delta(q,*,*),= \delta(q,(,)) = \{(q,\varepsilon)\}$
PDA 转 CFG
转换为 CFG 的 PDA 必须空栈方式接受,而非终态方式接受。
符号 $[pXq]$ 表示一个事件变元。它的涵义是:
-
从栈中净弹出符号
$X$ -
状态从开始状态
$p$转换到$q$,并且在转换到$q$状态之后,堆栈中的$X$完全被$\varepsilon$所替代。
也即:$[qXp]\to w \iff (q,w,X) \vdash^* (p,\varepsilon,\varepsilon)$
如果 $\mathrm{PDA} P=\left(Q, \Sigma, \Gamma, \delta, q_{0}, Z_{0}, \varnothing\right)$, 那么构造 $\mathrm{CFG}$
$G=\left(V, \Sigma, P^{\prime}, S\right)$, 其中 $V$ 和 $P^{\prime}$ 为
(1) $V=\{[q X p] \mid p, q \in Q, X \in \Gamma\} \cup\{S\}$
(2) 对 $\forall p \in Q$, 构造产生式 $S \rightarrow\left[q_{0} Z_{0} p\right]$;
(3 对 $\forall\left(p, Y_{1} Y_{2} \cdots Y_{n}\right) \in \delta(q, a, X)$, 构造 $|Q|^{n}$ 个产生式
$$
\left[q X r_{n}\right] \rightarrow a\left[p Y_{1} r_{1}\right]\left[r_{1} Y_{2} r_{2}\right] \cdots\left[r_{n-1} Y_{n} r_{n}\right]
$$
以空栈方式接受的 PDA,从栈中一个一个地弹出它的栈符号,会在输入带上一部分一部分地消耗输入串。这两种作用可以看成是相互抵消的作用。为了从栈中完全地弹出某一个栈符号,需要从输入带上消耗掉一部分输入串。那么消耗掉的输入串,与从栈中弹出的栈符号,是一种对应关系。如果将栈中的栈符号看作一种变元,就相当于从栈符号的变元,可以派生出来被消耗掉的输入带上的那部分输入串。我们就利用这样的方式,去构造一个能够表示 PDA 弹空栈的文法。文法的变元就对应了 PDA 的栈符号。但是因为弹出的栈符号之前和之后的状态如果不同的话,所消耗掉的输入串可能不一样。所以我们连同弹出这个栈符号之前和之后的那个状态,一起定义为文法的变元。比如如果从栈弹出 $X$,之前和之后的状态分别为 q 和 p,那么我们定义一个变元 qXp,从 q 状态弹出 X 到 p,会消耗掉一些输入串,这些输入串刚好就对应了这个变元所能派生出来的那些字符串。在 PDA 中为了弹出某一个栈符号,它的第一步可能是利用了某一个动作将这个栈符号,不如 X 替换为其它的一些栈符号的串,然后再一步一步地弹出这些栈符号。那么我们可以利用这个动作去定义一组产生式,将这些栈符号串所对应的变元,作为要弹出的变元的定义。那么有了变元之后,我们定义文法的产生式就根据 PDA 的动作,如果处在 q 时,当前读入的字符串是 A,A 可能是字符,也可能是空串,而栈顶是 X,那么相当于我们要将 X 弹出,但是第一步是将 X 替换为 Y1, Y2, … Yn, 而状态先变成了 p,我们就通过这一个动作去构造一组产生式。那么我们构造的产生式可以这样来理解:
从状态 q 弹出 X 能够到达某一个状态 $r_n$ ,他所消耗的全部输入串,由它能够派生出来。派生的第一步是派生出字符 a,然后剩下的字符串交给 $Y_1$ 对应的变元…一直到 Y_n 对应的变元。而为了弹出 $Y_1$ 开始的那个状态,就是我们的状态所到的那个状态。弹出 Y1 之后的那个状态设为 r1,弹出 y1 之后准备弹 y2 之前的那个状态刚好是同一个 r1,以此类推:
$$
\left[q X r_{n}\right] \rightarrow a\left[p Y_{1} r_{1}\right]\left[r_{1} Y_{2} r_{2}\right] \cdots\left[r_{n-1} Y_{n} r_{n}\right]
$$
其中 $a \in \Sigma \cup\{\varepsilon\}, X, Y_{i} \in \Gamma$,都是栈符号。 而 $r_{i} \in Q$ 是 $n$ 次 $|Q|$ 种 状态的组合,也即 $r_1$ 是所有的 Q 的可能,$r_2$ 也是所有的 Q 的可能… 所以一共是 $Q^n$ 个产生式。若 $i=0$, 为 $[q X p] \rightarrow a .$
文法的开始,刚好是从 q0,将栈底符号全部弹出之后,所消耗的串( $S \rightarrow\left[q_{0} Z_{0} p\right]$,p 是 Q 中全部的状态。$[q_0Z_0p]$ 的含义就是 PDA 从 $q_0$ 开始状态,完全地弹出 $Z_0$ 栈底符号,所消耗的输入串所对应的变元,而之后到达的状态是不知道的,所以定义为 $q \in Q$,也就是任何一个状态都可以。也就是说,由多少个状态,就要增加多少个开始符号的产生式);
【例子】PDA 的转移函数如下:
$1: \delta(q, 1, Z)=\{(q, X Z)\}$ $2: \delta(q, 1, X)=\{(q, X X)\}$ $3: \delta(q, 0, X)=\{(p, X)\}$ $4: \delta(q, \varepsilon, X)=\{(q, \varepsilon)\}$ $5: \delta(p, 1, X)=\{(p, \varepsilon)\}$ $6: \delta(p, 0, Z)=\{(q, Z)\}$
分析:
首先,我们要定义文法的开始符号 S。$S\to [qZ\{所有的p\}]$ (它的 $q_0$ 刚好是 q,$Z_0$ 刚好是 Z)
而所有的 $p$ 就是两种:$p,q$,因此展开:
-
$S\to[qZp]$ -
$S\to[qZq]$
下面我们来看所有 $\delta$ 产生式。
$1: \delta(q, 1, Z)=\{(q, X Z)\}$,对应的变元是 $q$,为了弹出 $Z$,可能到达某个状态 $?$,而它消耗一个字符 $1$,然后将 $Z$ 替换为 $XZ$。记作 $[qZ?] \to 1[\_X\_][\_Z\_]$。虽然弹出整个 $Z$ 的状态 $?$ 是未知的,但我们知道消耗 $1$ 到达的状态是 $q$,填上去就是 $[qZ?] \to 1[qX\_][\_Z\_]$,剩下的三个空是所有的可能。而为了满足变换的一致性,前两个 $\_$ 是同一个状态,$?$ 和最后一个 $\_$ 是同一个状态。也即:$[qZ{\color{red}m}] \to 1[qX{\color{blue}n}][{\color{blue}n}Z{\color{red}m}]$,由于有两个状态,所以一共有四种情况,即组合有 $mn = pp,pq,qp,qq$
即:
$$
\begin{array}{l}
{[q Z q] \rightarrow 1\left[q X_{0} q\right][q Z q]} \\
{[q Z q] \rightarrow 1[q X p][p Z q]} \\
{[q Z p] \rightarrow 1[q X q][q Z p]} \\
{[q Z p] \rightarrow 1[q X p][p Z p]}
\end{array}
$$
2型语言的泵引理(证明不是CFL)
构造图灵机
【例子】设计图灵机接受 $a^nb^n,n\geq 1$。
分析:
最初带:
aaaaa...abbbbb...bBBBBBBBB...
|-------||-------|
n个a n个b
思路:
-
将最左 a 改为 x,最左b 改为 y。
-
如果在搜索最左 y 时读到 B,则说明 y 的数量比 a 少,不接受。
-
如果在搜索最左 a 时读不到 a,且右边无 b,则接受。否则仍有 b,说明 b 比 a 多不接受。
【例子】设计图灵机接受 $0^n1^n2^n,n\geq 1$
【例子】设计图灵机接受 $a(a+b)^*$
分析:
b/b,R
a/a,R a/a,R B/B,R
[]------->[ ]-------->[[]]
