«自动机理论、语言和计算导论»笔记：第八章 图灵机

图灵机

图灵机（Turing Machine, TM）的组成：

• 一个有限状态控制器

  • 可以读取符号

  • 可以写入符号

  • 可以左移或右移指针

• 一条纸带，由有限个单格（cell）组成。可以从上面读写数据。单格可以为空。

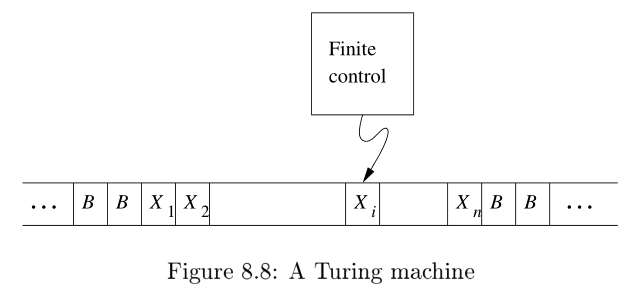
形式定义：

$$
M = (Q,T,\Sigma, \delta, q_0, B,F)
$$

$Q$: 有限状态集合

$T$：有限输入符号集合 $T \subseteq \Sigma$

$\Sigma$：有限带符号集合

$\delta$：转移函数

$q_0$：起始状态

$B$：空白符 $B\in \Sigma - T$

$F$：终态集合

两个性质：

1. 每个过程有穷可描述

2. 过程由离散、可机械执行的步骤组成

转移函数：

$$
\delta:Q\times \Sigma \to Q \times \Sigma \times \{L,R\}
$$

1function trans(presentState, currentSymbol){
2    return [nextState, outputSymbol, movement]
3}

例如 $\delta(q,a_i)\to(p,B,L)$，表示现态为 $q$，指针读到 $a_i$，则次态为 $p$，写入空，左移指针。

瞬时描述：$w_1qw_2$，表示正在读 $w_2$ 的第一个符号。$w_1w_2$ 是整个纸带的内容。

一旦进入终止状态，则认为串接受，并停机。

图灵机的停机问题：给定图灵机，是否存在判别程序，能判断该机器对串能否接受。此问题不可判定（无通用解）。

边的格式：$i/o,D$，$i$ 时输入 $o$ 是输出，$D$ 是移动方向。